Summary
This post contains a writeup and solutions for the Movement CTF held in 2022. Recently, I found an interesting bug hunting target deployed on the Aptos chain, so I started looking for Aptos smart contract wargames. I discovered this fun CTF from 2022 and decided to solve the challenges myself.
Background
It assumes basic knowledge of Move. Since the challenges are solved on the Aptos chain, you should also be familiar with the Aptos CLI. Exploit code for the solutions is available in the Github Repository linked for reference.
Challenge 1 - CheckIn
module ctfmovement::checkin {
// [...]
public entry fun get_flag(account: signer) acquires FlagHolder {
let account_addr = signer::address_of(&account);
if (!exists<FlagHolder>(account_addr)) {
move_to(&account, FlagHolder {
event_set: account::new_event_handle<Flag>(&account),
});
};
let flag_holder = borrow_global_mut<FlagHolder>(account_addr);
event::emit_event(&mut flag_holder.event_set, Flag {
user: account_addr,
flag: true
});
}
}
This challenge is very simple: just call the get_flag() function to solve it. Once it calls get_flag() function, it will obtains the flag.
Challenge 2 - HelloMove
public entry fun get_flag(account: &signer) acquires Challenge {
let addr = signer::address_of(account);
let res = borrow_global_mut<Challenge>(addr);
if (res.q1 && res.q2 && res.q3) {
event::emit_event(&mut res.flag_event_handle, Flag {
user: signer::address_of(account),
flag: true
})
}
}
Since the code for this challenge is quite long, I will analyze it in parts. The basic condition for obtaining the flag is to set all the variables q1, q2, and q3 inside the signer's Challenge struct to true. Let's look at each one step by step.
entry public fun hash(account: &signer, guess: vector<u8>) acquires Challenge{
let borrow_guess = &mut guess;
assert!(vector::length(borrow_guess) == 4, 0);
vector::push_back(borrow_guess, 109);
vector::push_back(borrow_guess, 111);
vector::push_back(borrow_guess, 118);
vector::push_back(borrow_guess, 101);
if (aptos_hash::keccak256(guess) == x"d9ad5396ce1ed307e8fb2a90de7fd01d888c02950ef6852fbc2191d2baf58e79") {
let res = borrow_global_mut<Challenge>(signer::address_of(account));
if (!res.q1) {
res.q1 = true;
}
}
}
To set q1 to true, it need to solve the hash function challenge. The problem is simple: append 4 bytes (109, 111, 118, 101 in ASCII) to the value received as guess, then compute the keccak256 hash and match it to the target hash.
This challenge can be solved easily by brute-forcing the 4 bytes until the target hash is reached. If you convert this logic to Python code using GPT, it would looks like the following.
Although the code generated by GPT looks a bit messy, it was the fastest way to find the value. It optimized the speed by creating a table of possible keywords, which allowed me to quickly discover the answer.
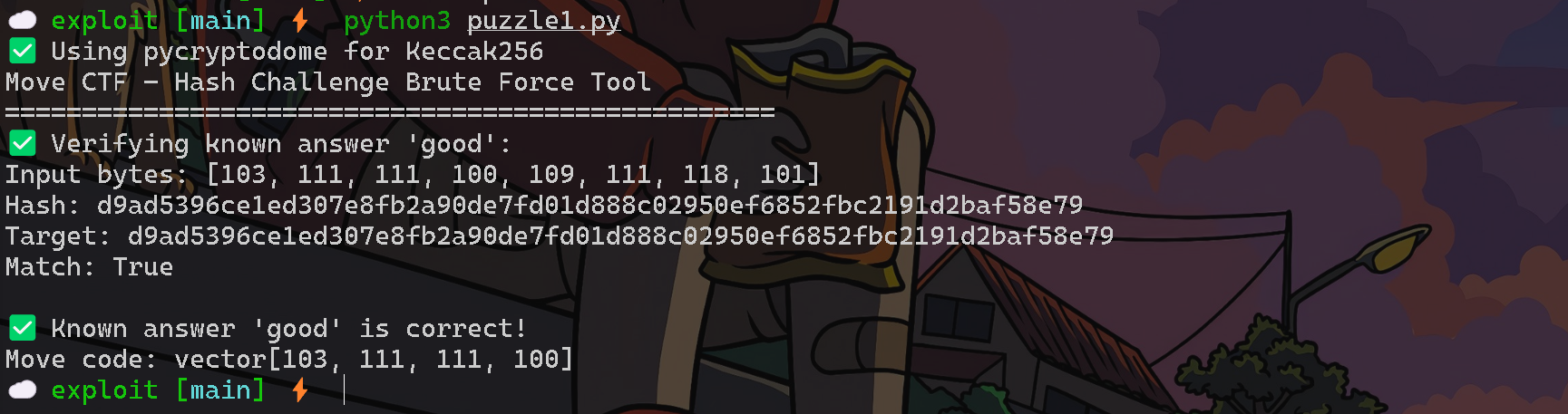
Since q1 has been solved, let's move on to solving q2.
public entry fun discrete_log(account: &signer, guess: u128) acquires Challenge {
if (pow(10549609011087404693, guess, 18446744073709551616) == 18164541542389285005) {
let res = borrow_global_mut<Challenge>(signer::address_of(account));
if (!res.q2) {
res.q2 = true;
}
}
}
This challenge requires reversing the modular exponentiation to find the exponent, i.e., solving a discrete logarithm problem. It can use the Baby-step giant-step (BSGS) algorithm to solve it. This algorithm splits the number into two parts, builds a table, and efficiently finds the discrete logarithm value. I used a Python library that implements this algorithm to solve the 2nd challenge.

lastly, let's move on to solving q3.
const Initialize_balance : u8 = 10;
// [...]
public fun init_challenge(account: &signer) {
let addr = signer::address_of(account);
let handle = account::new_event_handle<Flag>(account);
assert!(!exists<Challenge>(addr), 0);
move_to(account, Challenge {
balance: Initialize_balance,
q1: false,
q2: false,
q3: false,
flag_event_handle: handle
})
}
// [...]
public entry fun add(account: &signer, choice: u8, number: u8) acquires Challenge {
let res = borrow_global_mut<Challenge>(signer::address_of(account));
assert!(number <= 5, 0);
if (choice == 1) {
res.balance = res.balance + number;
} else if (choice == 2) {
res.balance = res.balance * number;
} else if (choice == 3) {
res.balance = res.balance << number;
};
if (!res.q3 && res.balance < Initialize_balance) {
res.q3 = true;
}
}
In this challenge, the initial balance is set to 10, and it needs to call the add function to make balance less than 10. Since there is no limit on the number of times you can call the function, it can solve the problem by causing an integer overflow. The number parameter is restricted, so the fastest way to trigger an overflow is to use the shift operation as your choice.
Since 10 in binary is b1010, it can cause an overflow of the u8 type by performing the shift operation 7 times.
After solving the q1, q2, and q3 challenges as described above, it can obtain the flag by calling the get_flag() function.
Challenge 3 - SimpleSwap
public fun get_flag(sender: &signer) acquires FlagHolder {
let simple_coin_balance = coin::balance<SimpleCoin>(signer::address_of(sender));
if (simple_coin_balance > (math::pow(10u128, 10u8) as u64)) {
let account_addr = signer::address_of(sender);
if (!exists<FlagHolder>(account_addr)) {
move_to(sender, FlagHolder {
event_set: account::new_event_handle<Flag>(sender),
});
};
let flag_holder = borrow_global_mut<FlagHolder>(account_addr);
event::emit_event(&mut flag_holder.event_set, Flag {
user: account_addr,
flag: true
});
} else {
abort EInsufficientAmount
}
}
This challenge implements a simple swap mechanism. Rather than find a vulnerability, it is difficult to analyze it. If you are solving this challenge, make sure to review the code carefully.
To obtain the flag, you need to hold SimpleCoin in an amount greater than math::pow(10u128, 10u8).
public fun claim_faucet(sender: &signer, amount: u64) acquires CoinCap {
let coins = mint<TestUSDC>(amount);
if (!coin::is_account_registered<TestUSDC>(signer::address_of(sender))) {
coin::register<TestUSDC>(sender);
};
coin::deposit(signer::address_of(sender), coins);
}
The vulnerability in this challenge occurs inside the claim_faucet function. By repeatedly calling this function, it can mint unlimited TestUSDC tokens and use them for repeated swaps to obtain the desired amount of SimpleCoin.
/// Swap Y to X, Y is in and X is out. This method assumes amount_out_min is 0
public fun swap_exact_y_to_x<X, Y>(
sender: &signer,
amount_in: u64,
to: address
): u64 acquires Pool, SwapMeta {
let (fee_num, fee_den) = swap_utils::fee();
let coins = coin::withdraw<Y>(sender, amount_in);
let fee_amount = ((fee_num * (coin::value(&coins) as u128) / fee_den) as u64);
let fee_y = coin::extract(&mut coins, fee_amount);
deposit_fee_y<X, Y>(fee_y);
let (coins_x_out, reward) = swap_exact_y_to_x_direct<X, Y>(coins);
let fee_amount = ((fee_num * (coin::value(&coins_x_out) as u128) / fee_den) as u64);
let fee_x = coin::extract(&mut coins_x_out, (fee_amount as u64));
deposit_fee_x<X, Y>(fee_x);
let amount_out = coin::value<X>(&coins_x_out);
check_or_register_coin_store<X>(sender);
coin::deposit(to, coins_x_out);
if (coin::value(&reward) > 0) {
check_or_register_coin_store<SimpleCoin>(sender);
coin::deposit(signer::address_of(sender), reward);
} else {
coin::destroy_zero(reward);
};
amount_out
}
However, there are some caveats to note here. At first, I simply minted u64.max - 1 tokens and called the swap_exact_y_to_x function. But there are two major issues with this approach.
public fun get_amount_out_no_fee(
amount_in: u64,
reserve_in: u64,
reserve_out: u64
): u64 {
assert!(amount_in > 0, ERROR_INSUFFICIENT_INPUT_AMOUNT);
assert!(reserve_in > 0 && reserve_out > 0, ERROR_INSUFFICIENT_LIQUIDITY);
let amount_in = (amount_in as u128);
let numerator = amount_in * (reserve_out as u128);
let denominator = (reserve_in as u128) + amount_in;
((numerator / denominator) as u64)
}
When calculating the amount_out value using the get_amount_out_no_fee function, the amount_in parameter can trigger an integer overflow during the calculation of the denominator or numerator. Therefore, it should provide an appropriate value for amount_in.
/// Swap Y to X, Y is in and X is out. This method assumes amount_out_min is 0
public fun swap_exact_y_to_x_direct<X, Y>(
coins_in: coin::Coin<Y>,
): (coin::Coin<X>, coin::Coin<SimpleCoin>) acquires Pool, SwapMeta {
let amount_in = coin::value<Y>(&coins_in);
deposit_y<X, Y>(coins_in);
let (rout, rin) = pool_reserves<X, Y>();
let amount_out = swap_utils::get_amount_out_no_fee(amount_in, rin, rout);
let (coins_x_out, coins_y_out) = swap<X, Y>(amount_out, 0);
assert!(coin::value<Y>(&coins_y_out) == 0, ERROR_INSUFFICIENT_OUTPUT_AMOUNT);
coin::destroy_zero(coins_y_out);
let reward = if (swap_utils::is_simple_coin<X>()) {
let (reward_num, reward_den) = swap_utils::reward();
simple_coin::mint<SimpleCoin>((((amount_out as u128) * reward_num / reward_den) as u64))
} else {
coin::zero<SimpleCoin>()
};
(coins_x_out, reward)
}
Another issue is the swap_exact_y_to_x function include a fee. In this swap system, swapping a large amount of tokens in one direction results in an exponentially decreasing amount of tokens received, so the fee can be a significant obstacle. As a result, the value of amount_out may even become zero. Therefore, it is important to call the swap_exact_y_to_x_direct function, which does not use a fee.
By following this scenario, after minting a suitable amount of TestUSDC using the claim_faucet function and repeatedly swapping it to SimpleCoin via the swap_exact_y_to_x_direct function, you can obtain the flag.
Challenge 4 - SwapEmpty
public entry fun get_flag(account: &signer) acquires LiquidityPool {
let pool = borrow_global_mut<LiquidityPool>(@ctfmovement);
let c1 = coin::value(&pool.coin1_reserve);
let c2 = coin::value(&pool.coin2_reserve);
assert!(c1 == 0 || c2 == 0, 0);
event::emit_event(&mut pool.flag_event_handle, Flag {
user: signer::address_of(account),
flag: true
})
}
This is another swap challenge. In this problem, it needs to drain one of the two token reserves in the swap.
public fun get_amouts_out(pool: &LiquidityPool, amount: u64, order: bool): u64 {
let (token1, token2) = get_amounts(pool);
if (order) {
return (amount * token2) / token1
}else {
return (amount * token1) / token2
}
}
This challenge contains an inflation attack vector. The exchange rate for tokens is determined based on previous reserves. However, if an attacker swaps a large amount of tokens in one direction to increase the reserve and decrease the reserve of the opposite token, they can swap even more tokens in the opposite direction in the next swap.
Normally, to prevent this, the incoming token amount is added to the denominator reserve to block inflation attacks, but this challenge does not implement such a safeguard.
Therefore, by calculating the exchange rate for each swap and repeatedly swapping, it can drain one of the token reserves and obtains the flag.
Challenge 5 - MoveLockV2
public fun unlock(user : &signer, p : u128) : bool acquires Counter, FlagHolder {
let encrypted_string : vector<u8> = encrypt_string(BASE);
let res_addr : address = account::create_resource_address(&@ctfmovement, encrypted_string);
let bys_addr : vector<u8> = bcs::to_bytes(&res_addr);
let i = 0;
let d = 0;
let cof : vector<u8> = vector::empty<u8>();
while ( i < vector::length(&bys_addr) ) {
let n1 : u64 = gen_number() % (0xff as u64);
let n2 : u8 = (n1 as u8);
let tmp : u8 = *vector::borrow(&bys_addr, i);
vector::push_back(&mut cof, n2 ^ (tmp));
i = i + 5;
d = d + 1;
};
let pol : Polynomial = constructor(d, cof);
let x : u64 = gen_number() % 0xff;
let result = evaluate(&mut pol, x);
if (p == result) {
get_flag(user);
true
}
else {
false
}
}
// [...]
fun get_flag(account: &signer) acquires FlagHolder {
let account_addr = signer::address_of(account);
if (!exists<FlagHolder>(account_addr)) {
move_to(account, FlagHolder {
event_set: account::new_event_handle<Flag>(account),
});
};
let flag_holder = borrow_global_mut<FlagHolder>(account_addr);
event::emit_event(&mut flag_holder.event_set, Flag {
user: account_addr,
flag: true
});
}
The condition for solving this challenge is to break the unlock function. This module contains a variety of encryption algorithms.
fun increment(): u64 acquires Counter {
let c_ref = &mut borrow_global_mut<Counter>(@ctfmovement).value;
*c_ref = *c_ref + 1;
*c_ref
}
// [...]
fun seed(): vector<u8> acquires Counter {
let counter = increment();
let counter_bytes = bcs::to_bytes(&counter);
let timestamp: u64 = timestamp::now_seconds();
let timestamp_bytes: vector<u8> = bcs::to_bytes(×tamp);
let data: vector<u8> = vector::empty<u8>();
vector::append<u8>(&mut data, counter_bytes);
vector::append<u8>(&mut data, timestamp_bytes);
let hash: vector<u8> = hash::sha3_256(data);
hash
}
The key intention of this challenge is likely to match the seed. The seed function is composed of a timestamp value and a nonce that increases with each call (since the value increments one by one, I’ll refer to it as a nonce).
However, if an attacker creates a module and uses the same algorithm to derive the encrypted value in the same block, the seed value included in the encrypted value will be the same. In other words, the seed value is pseudo-random.
Therefore, by creating a module as above and generating the encrypted value, it can pass it to the unlock function to obtains the flag.
Conclusion
By solving this CTF, I learned how to write exploits on the Aptos chain. In fact, although the language differs from EVM chains, similar types of vulnerabilities are likely to occur. The writeup and solution code for this CTF can be found in the Github Repository.